こんにちはブログ担当のYです
今回は条件付き確率を使った問題を紹介します
スミスさんの子ども・1
スミスさんには子どもが2人いる
そのうちの1人が女の子だとするともう1人も女の子である確率は?
※女の子と男の子が生まれる確率は同じとする
1)100%
2)66%
3)50%
4)33%
5)25%
答え
4)33%
まず、男の子と女の子が生まれる確率が同じということから、子どもが2人いる場合の組み合わせは(男、男)、(男、女)、(女、男)、(女、女)の4通りになります。
そしてそのうちの1人が女の子であるという情報から(男、男)の組み合わせは除外され、もう1人が女の子である確率は1/3(33%)になります。
スミスさんの子ども・2
スミスさんには子どもが2人いる
そのうち1人は火曜日生まれの女の子である
もう1人も女の子である確率は?
※男の子と女の子が生まれる確率、各曜日で生まれる子どもの数は同じ
答え
13/27(約48%)
どこから出てきたかもわからないこの数字ですが、問題1と解き方は大体同じです
まず問題1と同様に男の子と女の子の生まれる確率は同じ、また各曜日で生まれる子どもの数も同じなので2人の子どもの組み合わせは(男、男)、(男、女)、(女、男)、(女、女)の4通りと、(月、月)、(月、火)、(月、水)……(日、日)の49通りを組み合わせた4×49=196通りとなります。
そのうち、片方が火曜日生まれの女の子である場合は(男、女)の場合(月、火)……(日、火)の7通り。
(女、男)の場合(火、月)……(火、日)の7通り。
(女、女)の場合(月、火)……(日、火)の7通りと(火、月)……(火、日)の7通りから2回数えてしまった(火、火)の分を引いて13通り
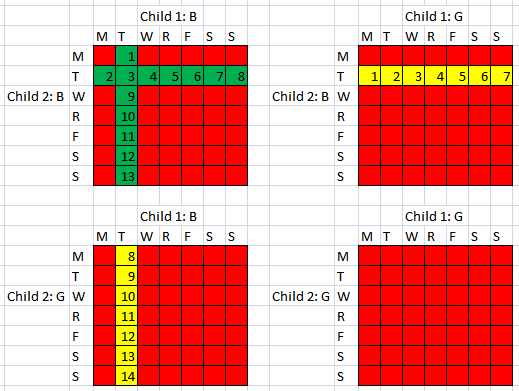
したがって片方が火曜日生まれの女の子であるのは196通り中27通りで、もう片方も女の子である、つまり(女、女)の組み合わせであるのは13通りなので答えは13/27となります。
確率って面白いですよね。ちなみにこの問題「火曜日生まれ」というのをさらに細かい条件にすることで確率を1/2に近づける事ができます。
例えば「1月1日に生まれた」という条件にすると729/1459(49.96%)になります。
これは確率を計算するときに両方が条件を満たす場合を2回数えてしまうので、1回分除外して考えるためです。
両方が条件を満たす可能性が低ければ低いほど本来の「子どもが女の子である確率」つまり1/2に近づいていくというわけです。
他の論理クイズの記事もCheck!




