こんにちはブログ担当のYです。
今回から人に話したくなる数学の小話を紹介します。
誕生日のパラドックス

僕今日が誕生日なんだ

偶然ね!私も今日が誕生日なの

同じ誕生日になる確率は365分の1だからすごい偶然だね!
なんていう経験ありませんか?
例えば学校の1クラスとして40人。
その中に誕生日が同じである2人がいる確率はどのくらいなのでしょうか。
1/365 × 40 = 40/365
このように単純に掛け算をして求められるわけではありません。
ではどのように求めるのでしょうか。
少人数の場合から考えてみましょう。
※今回の記事ではうるう年は考慮しておりません。
2人の場合
2人の誕生日が同じになる確率は1/365(約0.2%)になります。
3人の場合
仮にAさん、Bさん、Cさんとしましょう。
- AさんとBさんとCさんの誕生日が同じ
- AさんとBさんの誕生日が同じ
- AさんとCさんの誕生日が同じ
- BさんとCさんの誕生日が同じ
この4つの確率を全て足すことで3人の中に同じ誕生日の2人がいる確率を求められるのですが、もっと効率の良いやり方があります。
それは「3人全員の誕生日が異なる確率」
このように考えることで3人全員の誕生日が異なる確率を求めてそれを1から引くことで3人の中に誕生日が同じである2人がいる確率を求める事ができます。
364/365 × 363/365 ≒ 0.991 1 - 0.991 = 0.009
計算によって3人の中に同じ誕生日の2人がいる確率は約0.9%になる事がわかりました。
N人の場合
次に一般化してみます。
1<N<365を満たす整数Nについて、N人のなかに同じ誕生日の2人がいる確率は、3人の時と同様に全員の誕生日が異なる確率を1から引いて求めます。
1 - [364/365 × 363/365 × 362/365 × ・・・ × {365 - (N - 1)}/365]
というふうに一般化できます。
これに最初の状況の40人を当てはめて考えてみましょう。
1 - [364/365 × 363/365 × ・・・ × {365 - (40 - 1)}/365]
= 1 - (364/365 × 363/365 × ・・・ × 326/365)
≒ 1 - 0.109
= 0.891
したがって40人のクラスの中に誕生日が同じである2人の組が少なくとも一つある確率は約89%である事がわかりました。つまり同じ誕生の人の組がないほうが珍しいというわけですね。
ちなみに人数によってどのように変化しているかというと
| 人数 | 同じ誕生日の組がいる確率 |
| 2人 | 0.2% |
| 10人 | 12% |
| 20人 | 41% |
| 30人 | 71% |
| 40人 | 89% |
| 50人 | 97% |
| 60人 | 99.4% |
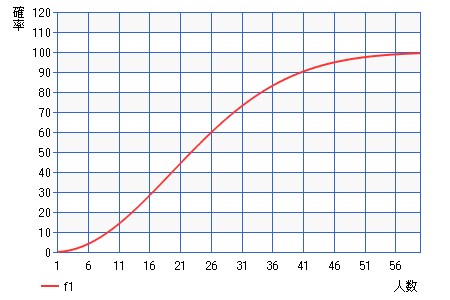
このように60人もいればほとんどの確率で同じ誕生日の組が存在することになります。
また、同じ誕生日の2人の組がいる確率が50%を超えるのは23人以上の時になります。
まとめ
365通りもあるのに40人の中に誕生日が同じ人がいる確率が89%もあるとは直感ではなかなか理解しづらいと思います。
この問題を知らない人に「誕生日が同じ2人の組がいる確率を50%以上になるには何人必要だと思う?」「30人の中に同じ誕生日の2人が含まれている確率はどのくらいだと思う?」などの質問をしてみると面白いかもしれません。
直感と違っていてとてもびっくりするでしょう。


