こんにちはブログ担当のYです。
今回も論理クイズを紹介します。
論理クイズ x マッチ棒パズル

ABCの3人がいます。
彼らは正直者か嘘つきのどちらかで、正直者は常に本当のことを言い、嘘つきは常に嘘をつきます。
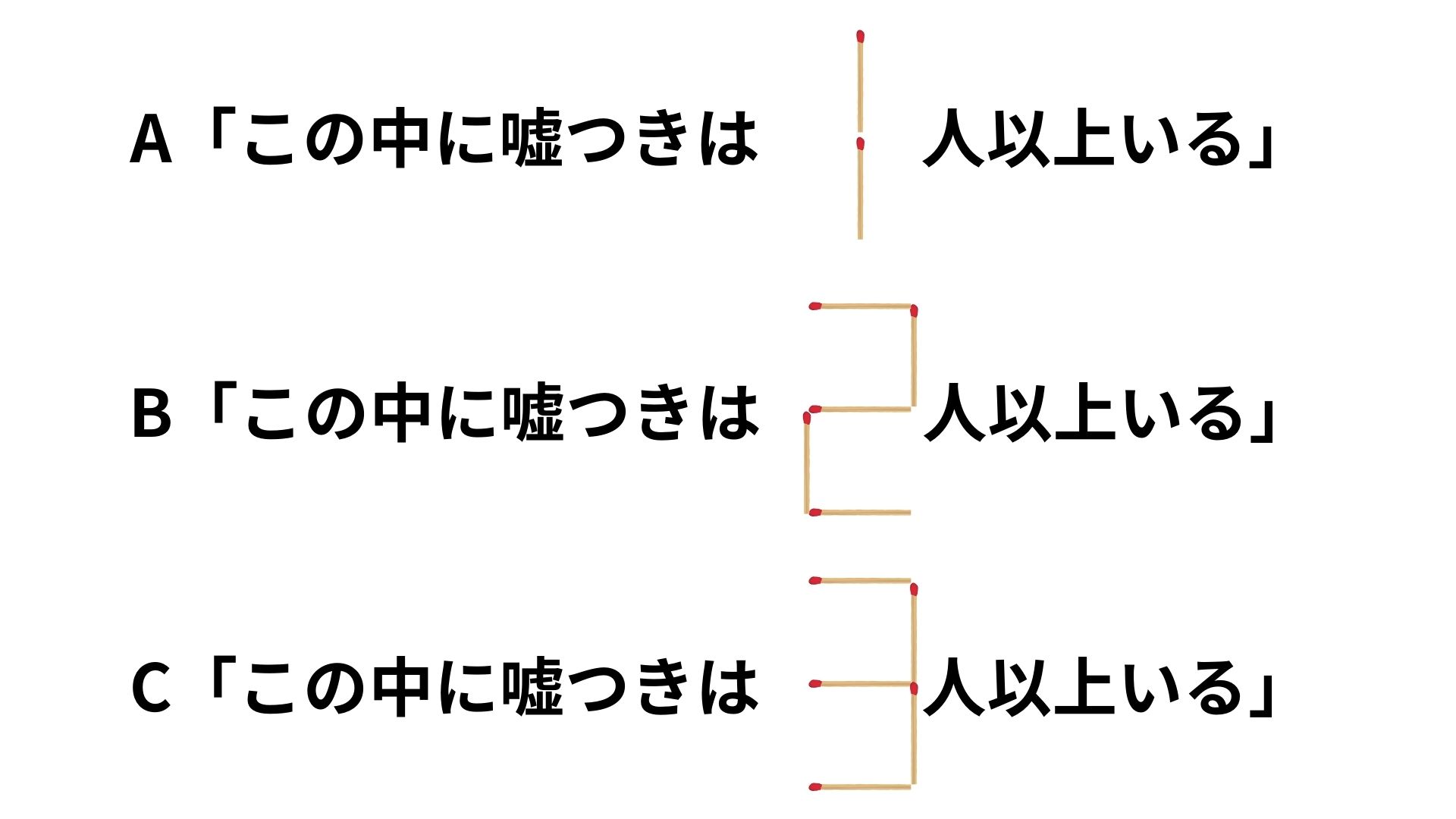
A「この中に嘘つきは1人以上いる」
B「この中に嘘つきは2人以上いる」
C「この中に嘘つきは3人以上いる」
この3人の発言は論理的に矛盾している。
上の画像をもとに、マッチ棒を一本だけ動かして、論理的矛盾を取り除いてください。
※マッチ棒は折ったり燃やしたりすることはできず、必ず数字として成り立つように動かしてください。
ヒント
論理的矛盾の解説
A「この中に嘘つきは1人以上いる」
B「この中に嘘つきは2人以上いる」
C「この中に嘘つきは3人以上いる」
この3人の発言の矛盾を解説します。
3人の中に嘘つきがいない場合
つまり全員が正直者ということになります。
しかし、全員の発言で「嘘つきがいる」という文章が含まれています。
嘘つきはいないので、矛盾が発生します。
3人の中に嘘つきがちょうど1人の場合
文章から、Aだけが正直者で、BとCは嘘つきになります。
しかし、嘘つきは1人だけなので、矛盾が発生します。
3人の中に嘘つきがちょうど2人の場合
文章から、AとBが正直者で、Cは嘘つきになります。
しかし、嘘つきはちょうど2人なので、矛盾が発生します。
3人全員が嘘つきの場合
全員の文章が正しいです。
しかし、全員が嘘つきなので矛盾が発生します。
以上より、初めの状態だとどのような場合でも矛盾が発生してしまいます。
マッチ棒を1本だけ動かして、矛盾を取り除いてください。
答え
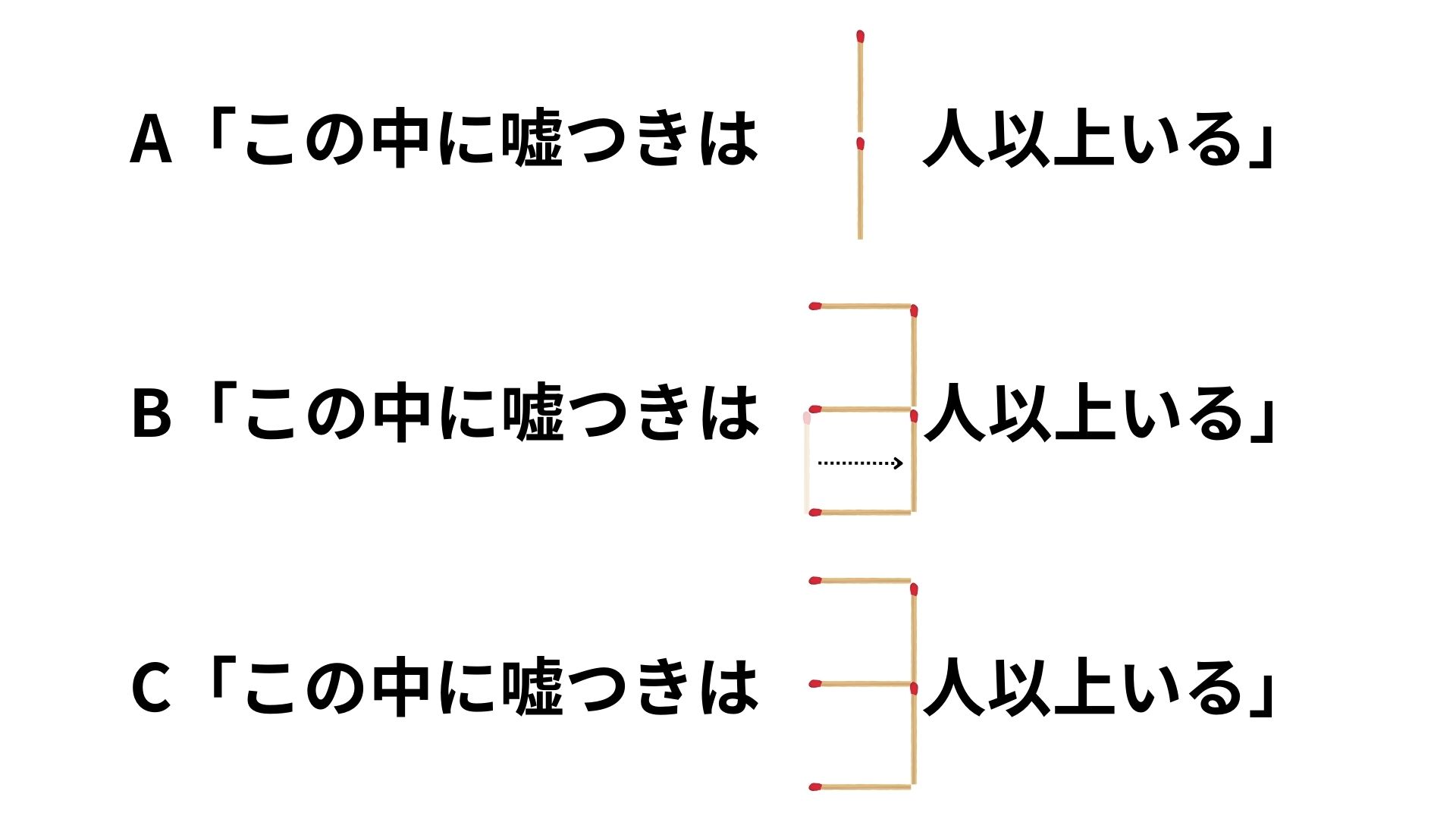
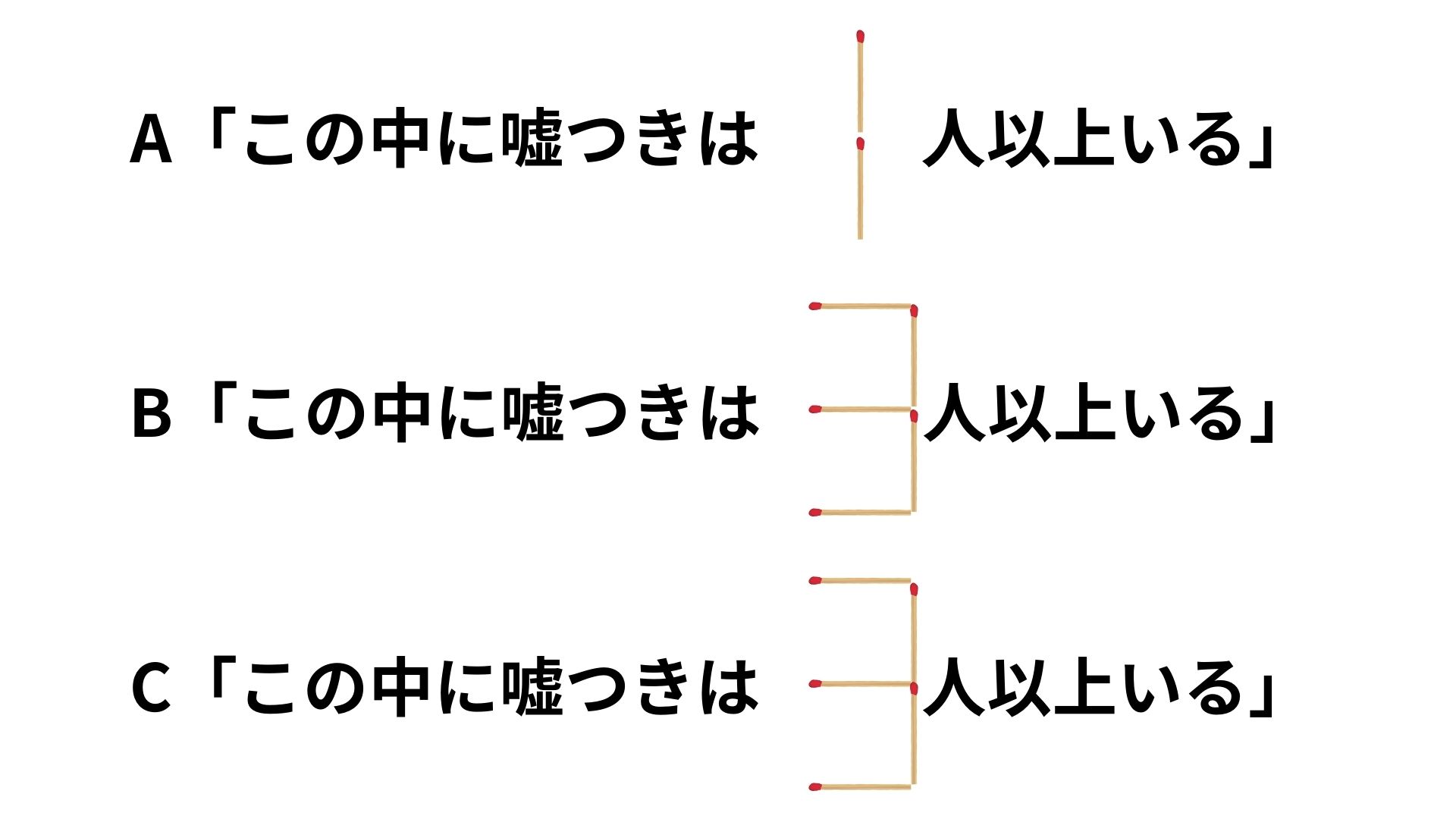
解説
A「この中に嘘つきは1人以上いる」
B「この中に嘘つきは3人以上いる」
C「この中に嘘つきは3人以上いる」
マッチ棒を動かした後の文章は以上のようになります。
ヒントの時と同様に、場合分けして考えてみましょう。
3人の中に嘘つきがいない場合
つまり全員が正直者ということになります。
しかし、全員の発言で「嘘つきがいる」という文章が含まれています。
嘘つきはいないので、矛盾が発生します。
3人の中に嘘つきがちょうど1人の場合
文章から、Aだけが正直者で、BとCは嘘つきになります。
しかし、嘘つきは1人だけなので、矛盾が発生します。
3人の中に嘘つきがちょうど2人の場合
文章から、Aだけが正直者で、BとCは嘘つきになります。
嘘つきはちょうど2人なので、問題ありません。
3人全員が嘘つきの場合
全員の文章が正しいです。
しかし、全員が嘘つきなので矛盾が発生します。
したがって、Bの文章の2を3にすることで、全体の矛盾を取り除くことができました。
他の論理クイズの記事もCheck!