こんにちはブログ担当のYです
今回は帽子の色当ての論理クイズを紹介します
帽子の色当てゲーム
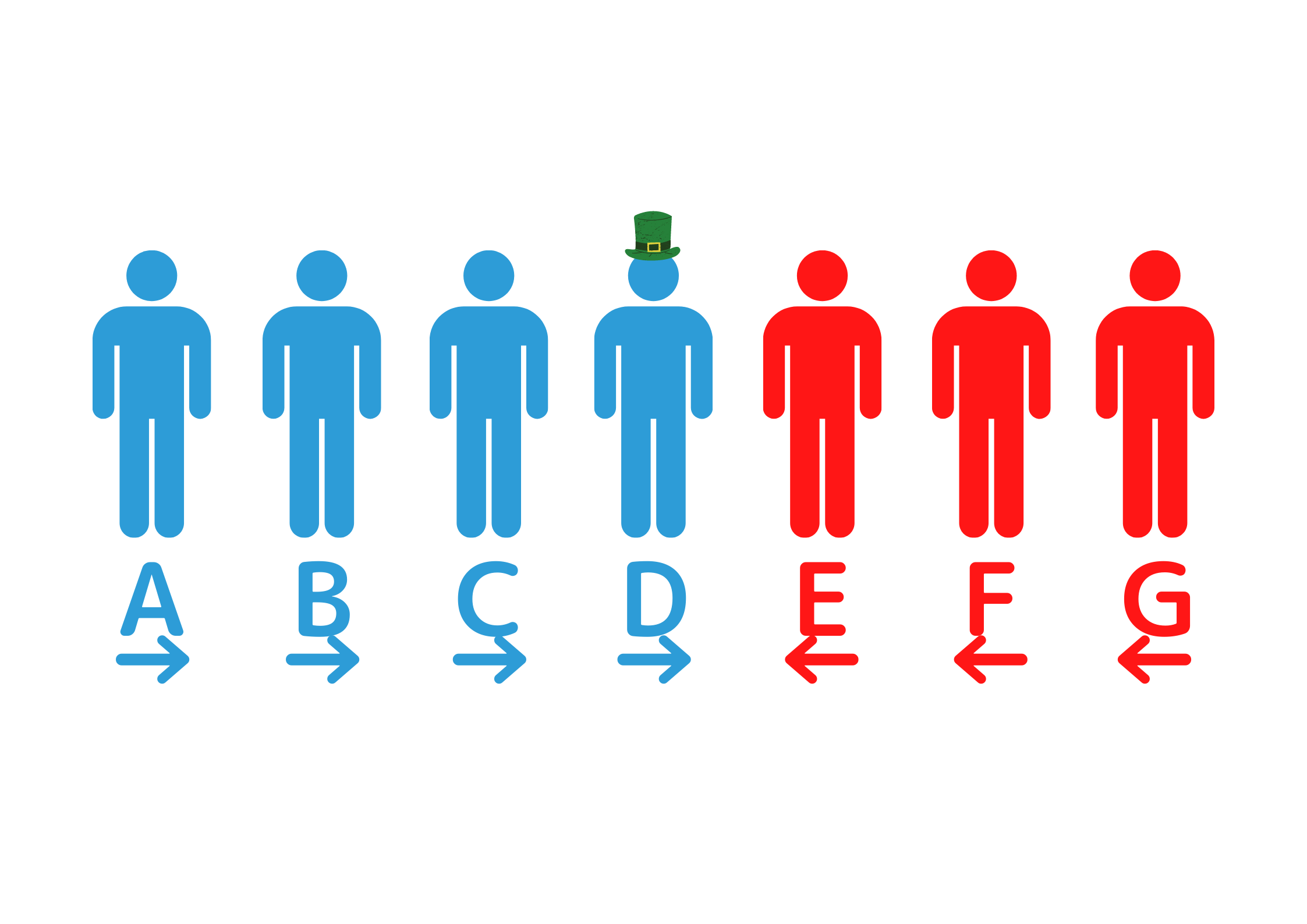
図のように7人が並んでいます
7人のうち2人は帽子をかぶっておらず、5人は緑か黒の帽子をかぶっています
また、Dは緑色の帽子をかぶっています
図の通りABCDの4人は自分より右側の全員の頭が見えていて、EFGの3人は自分より左側の全員が見えているとします
A「私は緑と黒の帽子が同じ数だけ見えます」
B「私は黒の帽子が緑の帽子の2倍の数見えます」
F「私は緑の帽子が黒の帽子の2倍の数見えます」
さて、誰が何色の帽子をかぶっているでしょう
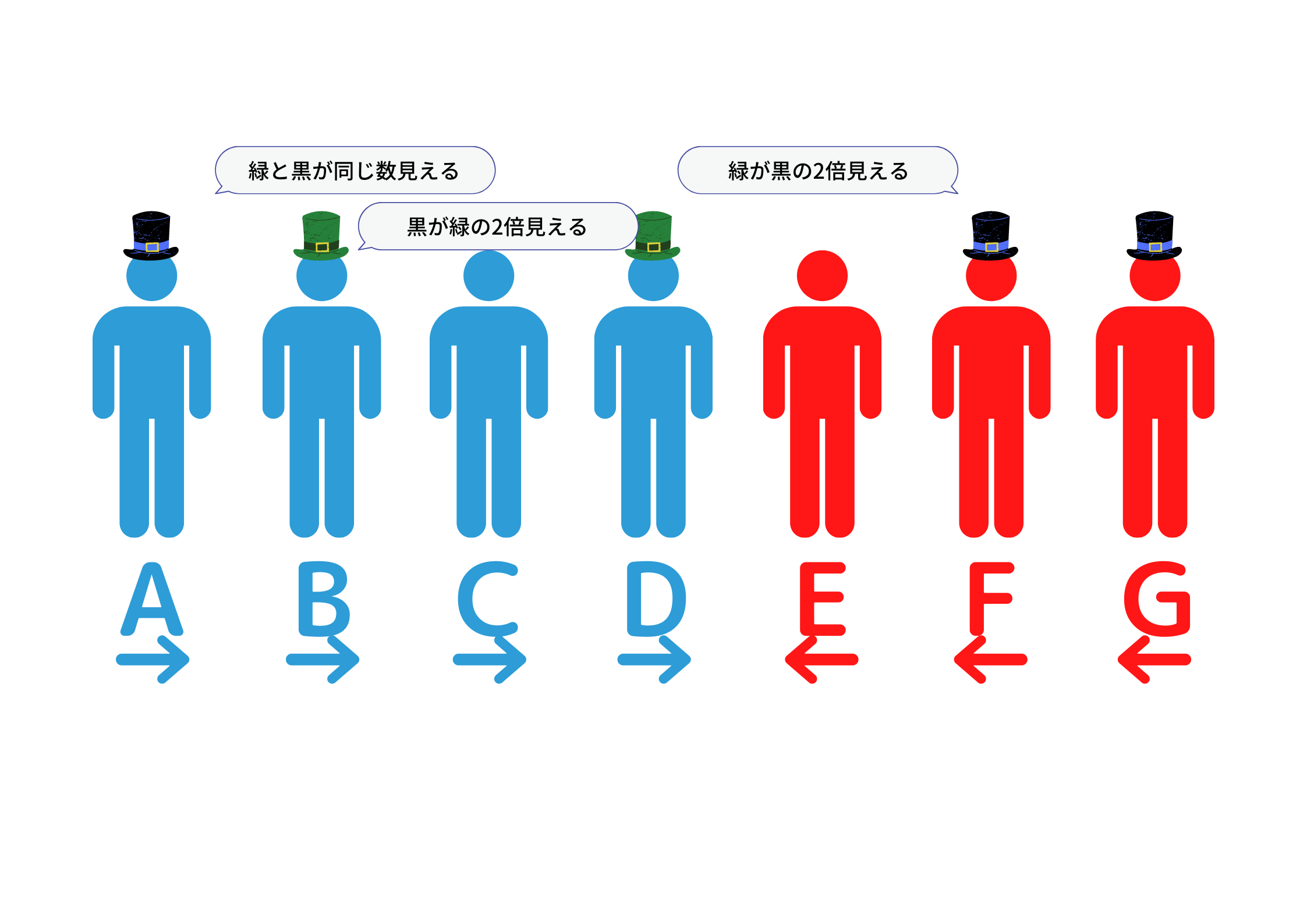
答え
A:黒
B:緑
C:何もかぶっていない
D:緑
E:何もかぶっていない
F:黒
G:黒
手順1
まず、Aは残りの6人の帽子が全て見える状況で、「緑と黒が同数見える」と言っています
帽子は全部で5つなので、Aが偶数個の帽子を見るためには、Aは帽子をかぶっていなければなりません
また、B〜Gの6人のうち2人が緑の帽子、2人が黒の帽子、2人が帽子をかぶっていないことがわかります
手順2
Bは黒が緑の2倍見えているということと、手順1で分かったことを踏まえると、Bは緑が1つ、黒が2つ見えていることになります
つまりBは緑色の帽子をかぶっていることが分かります
手順3
Fが緑の帽子を黒の帽子の2倍の数見えるためには、BとDの2つの緑に加えて1つの黒の帽子が見えていなければなりません
Aは帽子をかぶっているので、それが黒の帽子であることが分かります
また、CとEは帽子をかぶっていないことが分かります
手順4
ここでAとBの発言に戻ると、AとBはそれぞれ黒の帽子が2つ見えていることが分かります
また、CとEは帽子をかぶっておらず、Dは緑の帽子をかぶっています
つまりFとGは黒の帽子をかぶっていることが分かります
以上より、A・F・Gの3人が黒の帽子、B・Dの2人が緑の帽子、C・Eの2人は帽子をかぶっていないということが分かりました
他の論理クイズの記事もCheck!




