こんにちはブログ担当のYです。
今回も論理クイズを紹介します。
帽子の数字当てゲーム

あなたは帽子の数字当てゲームに参加しました。
ゲームのルールは以下の通りです。
- 参加者はあなたを含めて3人。
- 参加者にはそれぞれ正の整数が書かれた帽子が被せられる。
- 他の人の帽子の数字を見ることはできるが、自分の帽子の数字はわからない。
- 3つの数字のうちどれか1つは残り2つの数字の合計になっている 。(例)(4,6,10), (10, 20, 30) etc...
- 他の人の帽子の数字について発言してはいけない。
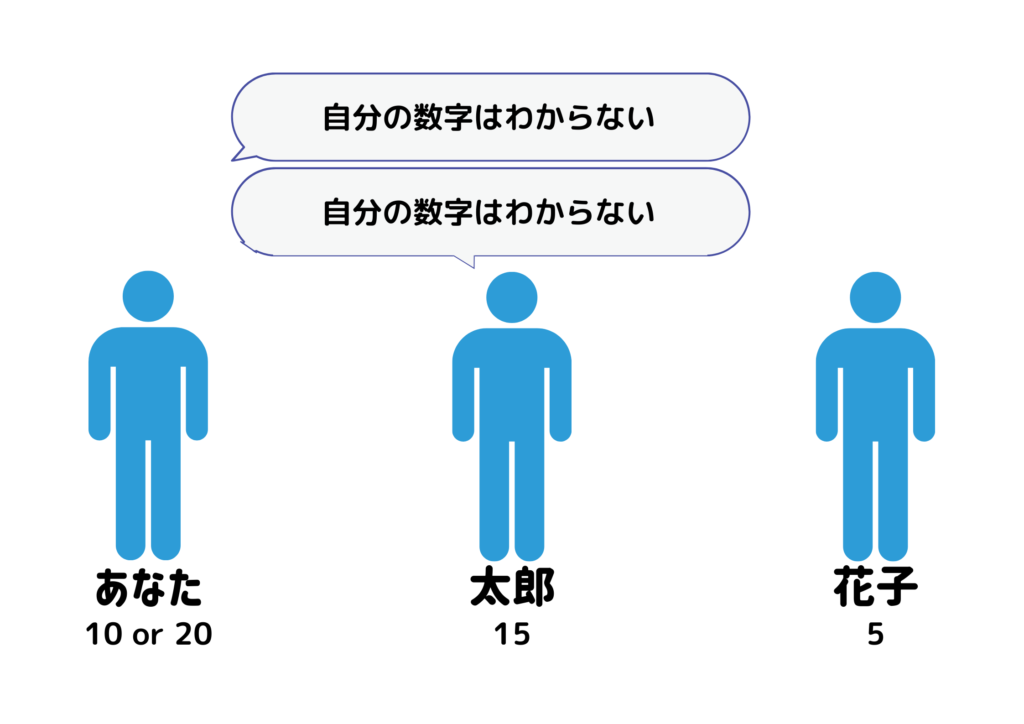
あなたは太郎さんと花子さんと一緒にゲームに参加しました。
ゲームが開始し、太郎さんの帽子には15が、花子さんの帽子には5が書かれていました。
この時点ではあなたの帽子の数字は10なのか、それとも20なのかわかりません。
あなたは「自分の数字はわからない」と発言しました。
すると太郎さんも「僕も自分の数字はわからないよ」と発言しました。
さて、あなたのかぶっている帽子の数字は10?それとも20?
※あなた以外の登場人物全員は正直かつ完璧な論理学者とします。(嘘をついていたり、推理が間違っていたりすることはありません。)
Puzzling.StackExchange[A harder version of a Richard Hess logical hat problem]
答え
20
解説
まず、この問題の状況で自分の数字がわかる場合とはどんな時かわかりますか?
それは見えている2つの数字が同じ数字の時です。
例えばあなたは残り2人の帽子の数字が両方とも100だということが見えたとします。
するとあなたの帽子の数字は200か0です。
しかし被せられた帽子の数字は「正の整数」なので、0はあり得ません。
そのため自分の帽子の数字が200だとすぐにわかります。
このように、残り2人の帽子の数字が同じだった場合、自分が0であるはずがないため、その2つの数字を合計した数字が自分の帽子の数字であるとわかります。
では、問題の状況を整理しましょう。
- 太郎さんは15
- 花子さんは5
- 自分の数字は10か20のどちらか
ここまでは開始直後にわかっていたことです。
これだけだと自分の数字が10なのか20なのか判断がつきません。
そのため、あなたは「わからない」と発言しました。
そして、その後太郎さんも「わからない」と発言しました。
ここで、あなたの数字が10の場合と20の場合で2つのパターンを分けて考えてみましょう。
あなたの数字が10の場合
あなた:10
太郎:15
花子:5
このような状況になっています。
ここで、太郎さんの気持ちになって考えてみましょう。
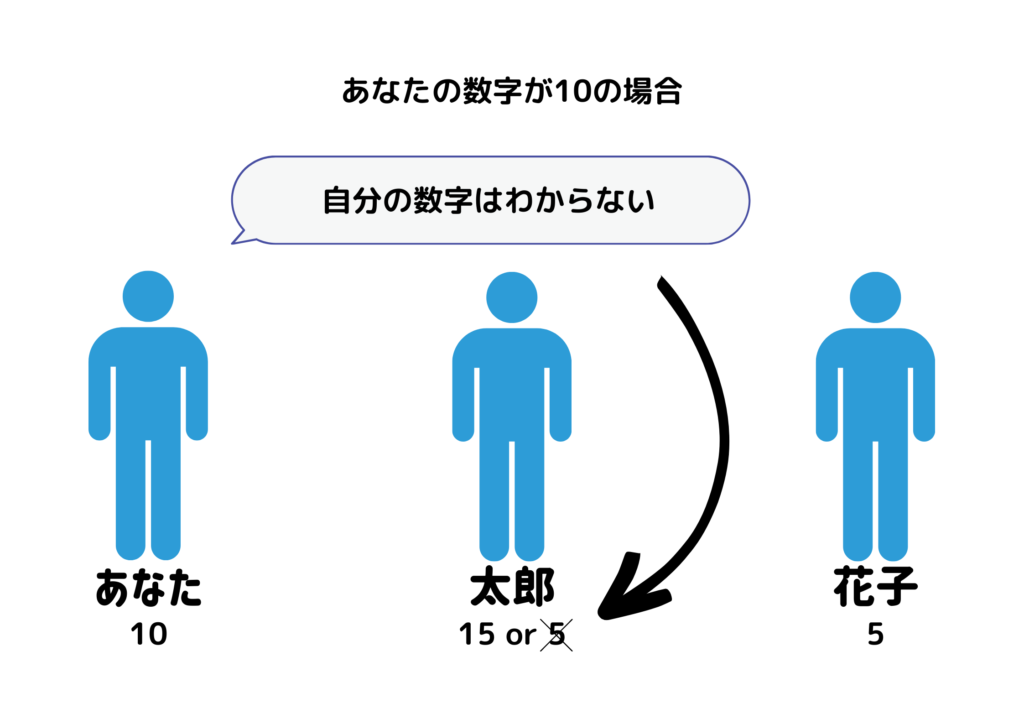
太郎さんからは10と5が見えています。
そのため、数字の組み合わせは(10, 15, 5)か(10, 5, 5)のどちらかだとわかります。
もし(10, 5, 5)の組み合わせだった場合、「あなた」が見えている2つの数字が同じであるため、自分の数字がわかるはずです。
しかし、「あなた」は「自分の数字がわからない」と発言しました。
この時点で太郎さんは自分の数字が5ではなく15だとわかります。
そのため、その後太郎さんが「自分の数字がわからない」と発言したことと辻褄が合いません。
したがって、あなたの数字が10であるという仮定がまちがっていることがわかりました。
あなたの数字が20の場合
あなた:20
太郎:15
花子:5
このような状況になっています。
ここでもまた、太郎さんの気持ちになって考えてみましょう。
ここでは、太郎さんは20と5が見えているため、数字の組み合わせは(20, 25, 5)か(20, 15, 5)のどちらかです。
どちらの組み合わせだとしても、「あなた」が開始時に数字を当てることはできません。
つまり「あなた」の「自分の数字がわからない」という発言は太郎さんにとってはヒントにはならず、太郎さんも数字がわからないままです。
そのため、太郎さんも「自分の数字がわからない」と発言しました。これに矛盾はありません。
まとめ
あなたの数字は初めの時点では10なのか20なのかわかりませんでした。
しかし、あなたの数字が10の場合、あなたが「わからない」と発言した時点で太郎さんは自分の数字がわかるはずです。
問題の状況では、太郎さんは「わからない」と発言したため、あなたの数字が10ではなく、20であることがわかりました。
他の論理クイズの記事もCheck!





